What is the relationship among usage rating, minutes per game, and games played per season for the twenty most highly rated usage NBA players over the last five seasons? Our hypothesis was that higher usage rating will lead to higher minutes played and more games played. However, we thought that players with a high usage rating will rarely play a full 82 game season due to increased vulnerability to injury.
We examined the relationships among our variables by running a bivariate regression using usage rating and games played, and a multivariate regression that added minutes per game. The data supported our hypothesis, though not at a confidence interval of 90% or above. The underlying assumption is that a high level of involvement within a game as well as throughout the season for an individual player will likely be reflected in that player’s usage rating. More specifically, a high usage rating will likely be accompanied by above average playing time.
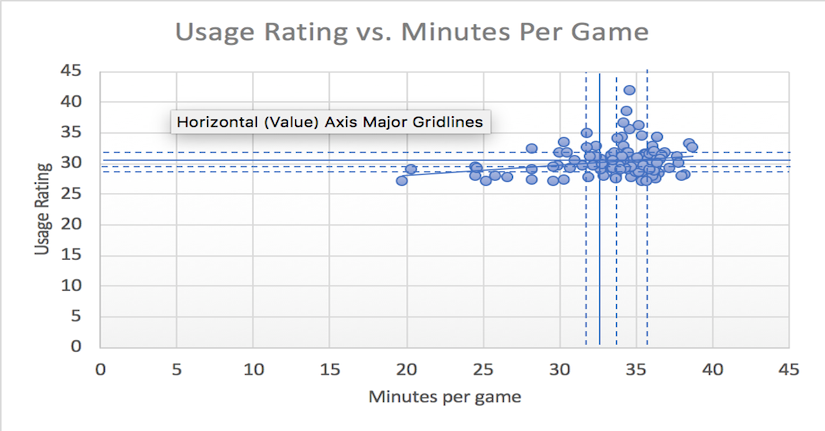
The independent variable, usage rating, identifies the most important players for each team. The dependent variables, minutes played per game and games played per season, measure a player’s involvement on the court. These measurements attempt to capture how a team tries to maximize the value of their key players through the time they spend on and off the court.
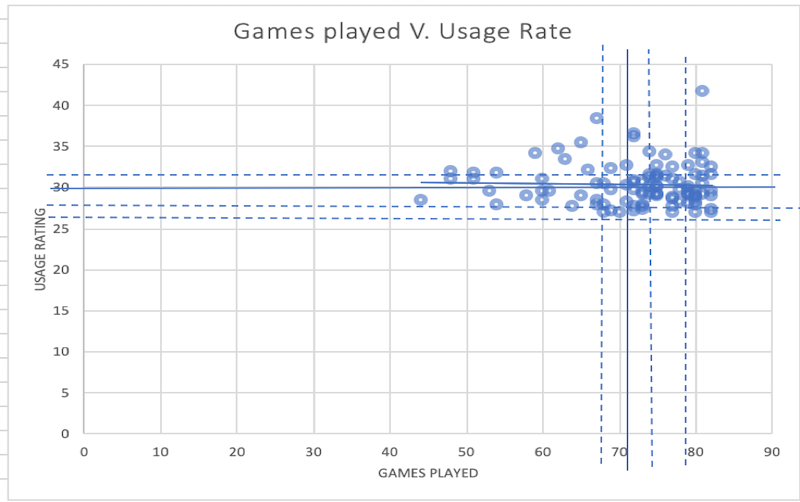
As expected, Figure 1 has a positively sloped trendline. Unexpectedly, Figure 2 has a slightly negative slope. We believe that this is indicative of the effect of usage rating on games played, because we focused on a sample of players whose teams attempt to maximize their utility in as many games as possible. We believe that if we expanded our sample size to all players in the league, the coefficient in Figure 2 would become positive (see Table 2).
The regression model can be expressed as follows:
Bivariate: Y = α0 + α1X1 + ε (1)
Multivariate: Y = α0 + α1X1 + α2X2 + ε (2)
where Y = usage rating, X1 = games played per season, and X2 = minute played per game.
| Y | X1 | X2 | |
| Mean | 30.34 | 71.94 | 33.489 |
| Standard Deviation | 2.5499 | 8.6335 | 3.6379 |
| Skewness | 1.4543 | -1.2411 | -1.6175 |
| Minimum | 26.9 | 44 | 19.7 |
| 25th Percentile | 28.8 | 68 | 32.2 |
| Median | 29.8 | 74 | 34.4 |
| 75th Percentile | 31.535 | 79 | 35.9 |
| Maximum | 41.7 | 82 | 38.7 |
| Correlation with Y | -0.03610 | 0.23457 | |
| Correlation with X1 | 0.11720 |
Likewise, we observed a negative regression coefficient, indicating a negative relationship between usage rating and games played. Initially, we hypothesized that the correlation between these two variables would be positive, as NBA teams will have more of an incentive to utilize players with high usage ratings in as many games as possible. However, the bivariate regression reflects the contrary: higher usage rating leads to a slightly lower number of games played. While this may hold true in some cases due to the risk for injury associated with higher usage rating, we believe this value may be inaccurate due to the low number of variables captured by the regression. This could be explained by omitted variable bias. Once we accounted for the control variable, minutes played per game, the regression coefficient for games played switched to a positive value.
Although we were able to capture the impact of the omitted variable bias in relation to minutes played per game, there are also several other omitted variables that could have a significant effect on this regression, including players’ health, sleep, and nutrition, and the front office’s influence on morale.
| Bivariate | Multivariate | |
| X1 | -0.00813 (0.02677) | 0.00129 (0.02744) |
| Control | N/A | 0.0641 (0.0448) |
| R2 | -0.00813 | 0.00131 |
Another limitation can be found in Table 2,
which displays very low R² values, meaning that our data was not very closely
clustered around our linear regression equation. We believe that this is
another indication of the high number of influential but not measurable omitted
variables when calculating sports statistics.
For example, we would expect players with a high defensive
workload to play fewer games, following the logic that an increased level of
involvement (on either end of the court) will lead to an increased risk of
injury, causing players to miss a few games over the course of the season.
Therefore, we would assume a negative correlation between usage rating and
defensive contribution.
Likewise, another potential omitted variable is the average number
of a team’s possessions per game. This statistic would reflect the pace at which
the team plays during a game, with a higher number of possessions indicating a
faster pace. We believe that a lower number of average possessions will lead to
both higher usage rating and higher games played, because the player will need
to use fewer possessions, and therefore less energy, to achieve the same usage
rating. This would also lower the risk for missing games, as we hypothesize
that greater amounts of play will lead to a greater risk for injury. Overall,
we would assume a negative correlation between the two: fewer team possessions
per game would likely increase usage
rating.
The outliers in our current sample are neither unexpected nor harmful to our results, and are
explainable. For example, unpredictable injuries explain our two largest
outliers for low games played, Chris Bosh and Kristaps Porzingis, each of whom
suffered season-ending injuries in multiple seasons. Tony Wroten, an outlier
for low minutes, spent the first half of the season coming off the bench before
excelling as a starter, leading him to have an unusually low number of minutes.
Russell Westbrook and James Harden, our two biggest outliers for usage rating, were
each tasked with being the sole major offensive force for his team.
We conclude that our results support our initial hypothesis: NBA
players with high usage ratings play both a high number of minutes per game and
a high number of games per season, though not all. The multiple regression
analysis supports this by demonstrating a positive correlation between usage
rating and games played, as well as usage rating and minutes played per game,
implying that all three variables move in the same direction. However, the
bivariate regression analysis displayed a negative correlation between usage
rating and games played, introducing some inconsistency to our data analysis.
Our analysis implies that, on average, NBA teams will maximize the playing time of individual players who possess high usage ratings, while ensuring some rest within a game or season to prevent major injuries. Knowing this can help organizations, opponents, and even fans to predict the type of roles and habits certain players may develop. To obtain more comprehensive results, similar research would need to be done with a much larger and more diverse sample of the league to account for the omitted variables that we were unable to capture. The results from such research would help to increase general understanding of the usage rating statistic, and further expand the realm of sports statistics.
This was written by Sam Lucas and Mary Ture.


