Around 10pm on Saturday night, after North Texas had just completed their 9-point upset over Purdue, the ESPN Tournament Challenge app sent a notification that out of 14.7 million brackets submitted to ESPN, a mere 1,039 remained perfect. Just for fun, I wanted to calculate how human judgement was performing against a simple coin toss.
2^12 yields that for 12 games, there are 4096 possible outcomes. Dividing 14.7 million by 4096 reveals that each outcome should be present ~3589 times, or about 3.45x as many perfect brackets as there were at that point in time. This trend continued to hold for a few games, before human perfect brackets started to outperform the coin toss again. By end of the first day of games, 14.7-million coin-flip brackets would have ~224 that remained perfect, compared to the 108 remaining. When the last brackets were finally busted late on the second day, human-picked brackets had once again become more effective.
Tournament Win Probability Swings:
Through the first 32 games, teams’ chances of winning the tournament have fluctuated quite a bit. Here’s an overview of the largest gains as a result of individual games, both by percent change and total increase:
By % Change:
| Rank | Game | Game | % Change |
| 1 | Oral Roberts | Ohio St. vs. Oral Roberts | 864.30% |
| 2 | Ohio | Virginia vs. Ohio | 345.42% |
| 3 | Abilene Christian | Texas vs. Abilene Christian | 281.36% |
| 4 | Oregon St. | Tennessee vs. Oregon St. | 236.54% |
| 5 | North Texas | Purdue vs. North Texas | 187.02% |
| 6 | Maryland | Maryland vs. Connecticut | 150.58% |
| 7 | UCLA | BYU vs. UCLA | 136.64% |
| 8 | Syracuse | SDSU vs. Syracuse | 119.41% |
| 9 | LSU | LSU vs. St. Bonaventure | 103.18% |
| 10 | Florida | Ohio St. vs. Oral Roberts | 97.83% |
By Total Increase:
| Rank | Game | Game | Total Increase |
| 1 | Gonzaga | Virginia vs. Ohio | 1.36% |
| 2 | Iowa | Iowa vs. GCU | 0.95% |
| 3 | Illinois | Tennessee vs. Oregon St. | 0.78% |
| 4 | Wisconsin | UNC vs. Wisconsin | 0.70% |
| 5 | Loyola Chicago | Loyola Chicago vs. Georgia Tech | 0.67% |
| 6 | Texas Tech | Texas Tech vs. Utah St. | 0.63% |
| 7 | Baylor | Purdue vs. North Texas | 0.61% |
| 8 | Illinois | Illinois vs. Drexel | 0.58% |
| 9 | Colorado | Colorado vs. Georgetown | 0.56% |
| 10 | Creighton | Virginia vs. Ohio | 0.47% |
If looking at the largest swings over the entire course of all 32 games:
By % Change:
| Rank | Team | % Change |
| 1 | Oral Roberts | 564.84% |
| 2 | Abilene Christian | 312.86% |
| 3 | Ohio | 221.61% |
| 4 | UCLA | 218.38% |
| 5 | Florida | 213.08% |
| 6 | Maryland | 163.56% |
| 7 | Oregon St. | 162.26% |
| 8 | North Texas | 142.71% |
| 9 | Creighton | 92.55% |
| 10 | Syracuse | 86.71% |
By Total Change:
| Rank | Team | Total Increase |
| 1 | Alabama | 1.108% |
| 2 | Texas Tech | 0.846% |
| 3 | Creighton | 0.756% |
| 4 | Wisconsin | 0.711% |
| 5 | Loyola Chicago | 0.681% |
| 6 | Florida | 0.565% |
| 7 | Arkansas | 0.549% |
| 8 | Colorado | 0.436% |
| 9 | LSU | 0.392% |
| 10 | UCLA | 0.388% |
If the percent change for each team is graphed, it forms a pretty nice pattern that makes it easy to see where major upsets occurred, along with how impactful an upset was for the rest of the field.
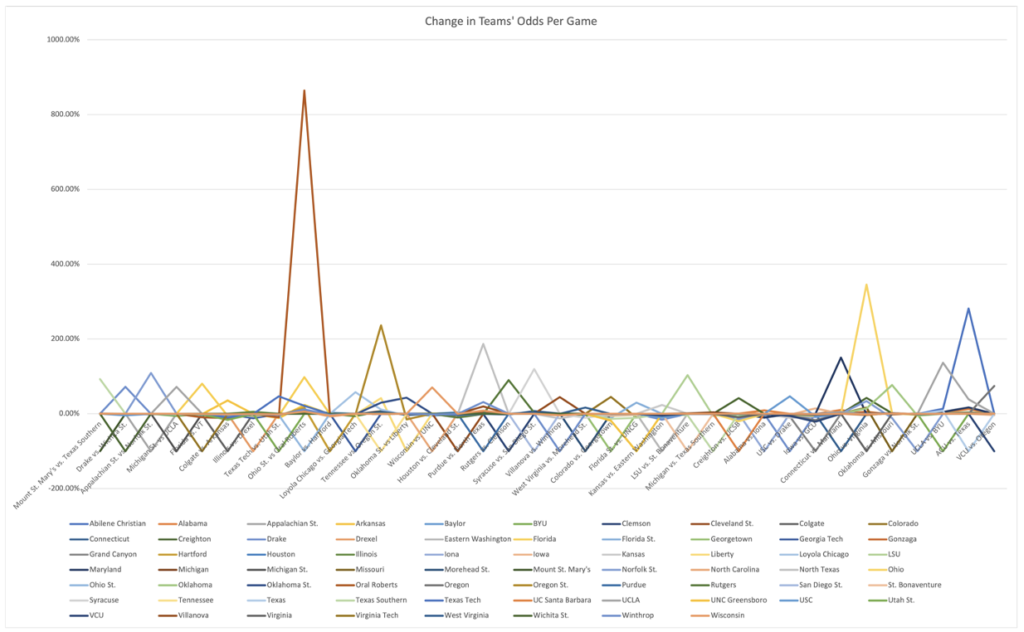
Overall, two games in the first round stand out as particularly impactful even for teams that did not play in them: #13 Ohio’s upset over #4 Virginia and #2 Oral Roberts upset over #2 Ohio State. In the case of the Ohio upset, Creighton (their opponent in the next game) will now no longer have to take on a Virginia team with better metrics (via KenPom and ESPN BPI) than Ohio. Their chances of winning the entire tournament increased .47% total as a result.

Further, Gonzaga, after their chances decreased throughout the day due to a lack of upsets in their region, went up 1.36% total again due to Virginia’s exiting the tournament.

And in the case of the Oral Roberts upset, Florida’s chances changed significantly, up 97%, due to now facing Oral Roberts rather than an Ohio State team with significantly better metrics.
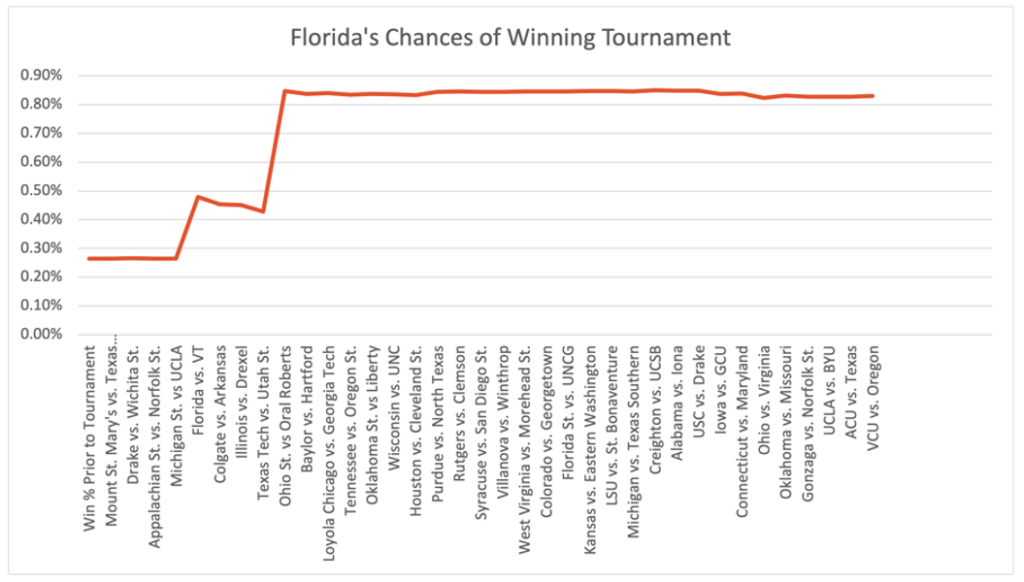
These probabilities all assume that metrics in this pandemic season are a measure of ability. They are and they, as we’ve seen, are not. It’s all part of why we watch and what leads to the Madness of March.
Notes on Methodology:
To calculate win probability for an individual match, KenPom’s Adjusted Efficiency Margin and ESPN’s BPI metrics are first used to determine an estimated point margin. Factors such as notable injuries and rest days are taken into account when generating the point margin. This point margin is then applied to a normalized distribution curve with a standard deviation of 11 (what KenPom uses to calculate its win probabilities). To come up with a team’s odds of winning the tournament, weighted averages of win probabilities against all possible teams in each round of the tournament are used. This yields similar results to FiveThirtyEight and other groups predicting tournament/round win probabilities.


